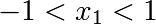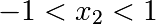2.7. Mathematical optimization: finding minima of functions¶

Authors: Gaël Varoquaux

Mathematical optimization deals with the problem of finding numerically minimums (or maximums or zeros) of a function. In this context, the function is called cost function, or objective function, or energy.

Here, we are interested in using scipy.optimize for black-box optimization: we do not rely on the mathematical expression of the function that we are optimizing. Note that this expression can often be used for more efficient, non black-box, optimization.

Prerequisites

Numpy, Scipy
matplotlib

2.7.1. Knowing your problem ¶

Not all optimization problems are equal. Knowing your problem enables you to choose the right tool.

Dimensionality of the problem

The scale of an optimization problem is pretty much set by the dimensionality of the problem, i.e. the number of scalar variables on which the search is performed.

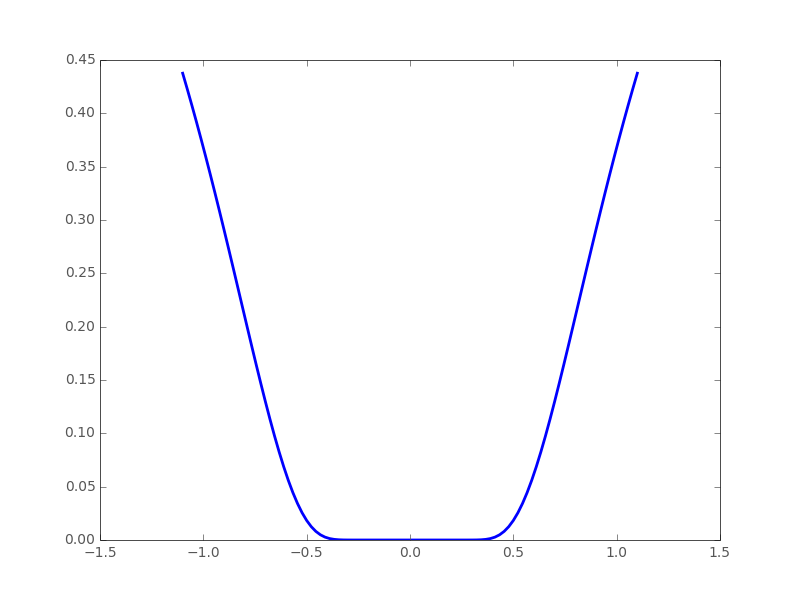
2.7.1.1. Convex versus non-convex optimization ¶

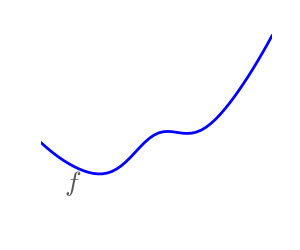A convex function:

f is above all its tangents.
equivalently, for two point A, B, f(C) lies below the segment [f(A), f(B])], if A < C < B

A non-convex function

Optimizing convex functions is easy. Optimizing non-convex functions can be very hard.

Note

It can be proven that for a convex function a local minimum is also a global minimum. Then, in some sense, the minimum is unique.

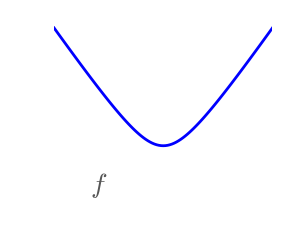
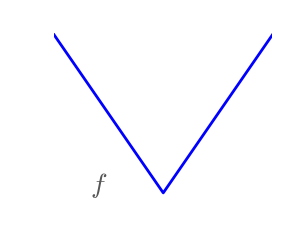
2.7.1.2. Smooth and non-smooth problems ¶

A smooth function:

The gradient is defined everywhere, and is a continuous function

A non-smooth function

Optimizing smooth functions is easier (true in the context of black-box optimization, otherwise Linear Programming is an example of methods which deal very efficiently with piece-wise linear functions).

2.7.1.3. Noisy versus exact cost functions ¶

Noisy (blue) and non-noisy (green) functions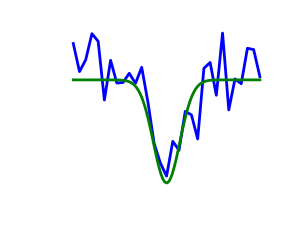

Noisy gradients

Many optimization methods rely on gradients of the objective function. If the gradient function is not given, they are computed numerically, which induces errors. In such situation, even if the objective function is not noisy, a gradient-based optimization may be a noisy optimization.

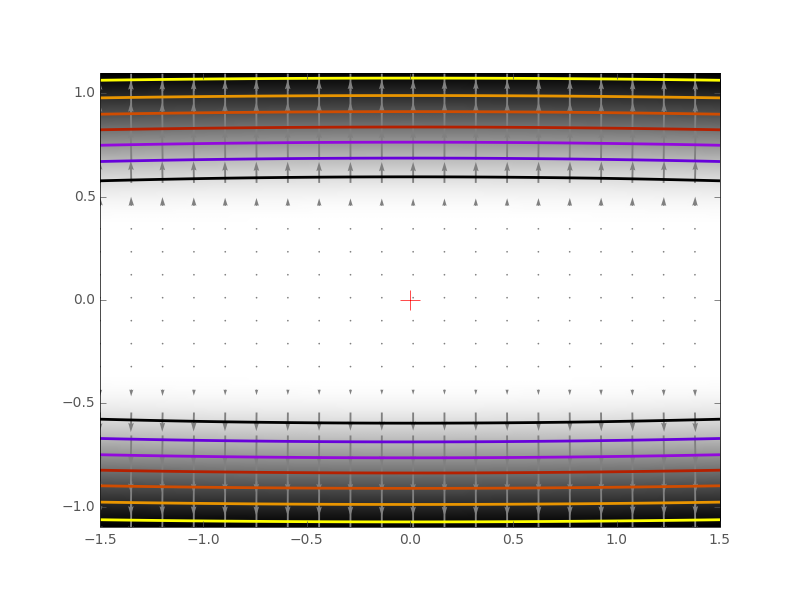
2.7.1.4. Constraints ¶

Optimizations under constraints

Here:

$-1 < x_1 < 1$

$-1 < x_2 < 1$

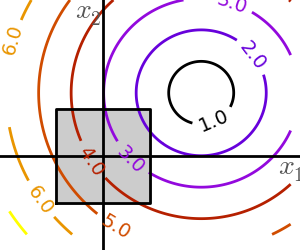2.7.2. A review of the different optimizers ¶

2.7.2.1. Getting started: 1D optimization ¶

Use scipy.optimize.brent() to minimize 1D functions. It combines a bracketing strategy with a parabolic approximation.

Brent’s method on a quadratic function: it converges in 3 iterations, as the quadratic approximation is then exact.
Brent’s method on a non-convex function: note that the fact that the optimizer avoided the local minimum is a matter of luck.

>>> fromscipyimportoptimize
>>> deff(x):
... return-np.exp(-(x-.7)**2)
>>> x_min=optimize.brent(f)# It actually converges in 9 iterations!
>>> x_min
0.699999999...
>>> x_min-.7
-2.1605...e-10

Note

Brent’s method can also be used for optimization constrained to an interval using scipy.optimize.fminbound()

Note

In scipy 0.11, scipy.optimize.minimize_scalar() gives a generic interface to 1D scalar minimization

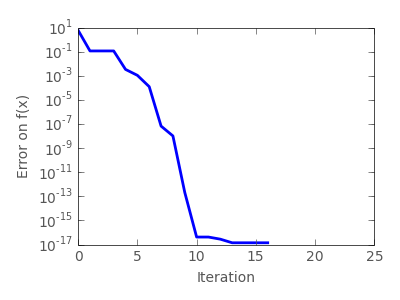
2.7.2.2. Gradient based methods ¶

2.7.2.2.1. Some intuitions about gradient descent¶

Here we focus on intuitions, not code. Code will follow.

Gradient descent basically consists in taking small steps in the direction of the gradient, that is the direction of the steepest descent.

**Fixed step gradient descent**¶
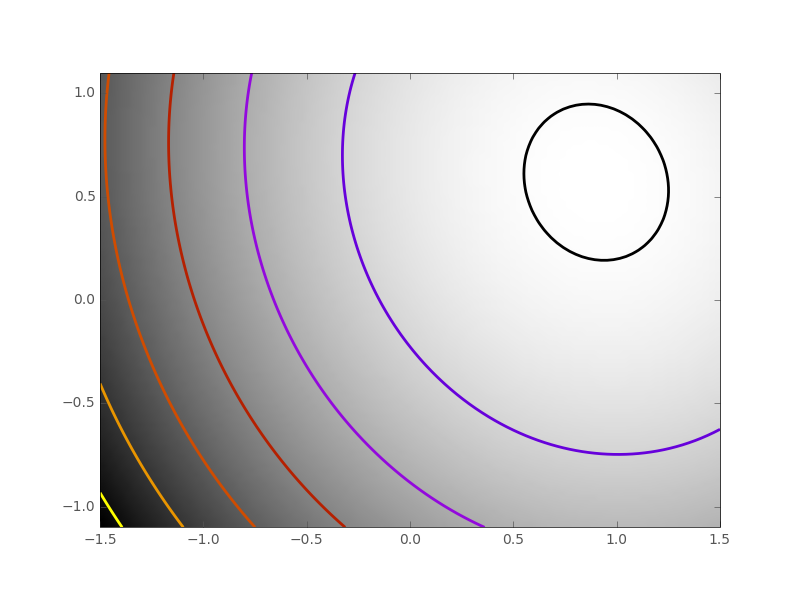
A well-conditionned quadratic function.
An ill-conditionned quadratic function. The core problem of gradient-methods on ill-conditioned problems is that the gradient tends not to point in the direction of the minimum.

We can see that very anisotropic (ill-conditionned) functions are harder to optimize.

Take home message: conditioning number and preconditioning

If you know natural scaling for your variables, prescale them so that they behave similarly. This is related to preconditioning.

Also, it clearly can be advantageous to take bigger steps. This is done in gradient descent code using a line search.

**Adaptive step gradient descent**¶
A well-conditionned quadratic function.
An ill-conditionned quadratic function.
An ill-conditionned non-quadratic function.
An ill-conditionned very non-quadratic function.

The more a function looks like a quadratic function (elliptic iso-curves), the easier it is to optimize.

2.7.2.2.2. Conjugate gradient descent¶

The gradient descent algorithms above are toys not to be used on real problems.

As can be seen from the above experiments, one of the problems of the simple gradient descent algorithms, is that it tends to oscillate across a valley, each time following the direction of the gradient, that makes it cross the valley. The conjugate gradient solves this problem by adding a friction term: each step depends on the two last values of the gradient and sharp turns are reduced.

**Conjugate gradient descent**¶
An ill-conditionned non-quadratic function.
An ill-conditionned very non-quadratic function.

Methods based on conjugate gradient are named with ‘cg’ in scipy. The simple conjugate gradient method to minimize a function is scipy.optimize.fmin_cg():

>>> deff(x):# The rosenbrock function
... return.5*(1-x[0])**2+(x[1]-x[0]**2)**2
>>> optimize.fmin_cg(f,[2,2])
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 13
        Function evaluations: 120
        Gradient evaluations: 30
array([ 0.99998968,  0.99997855])

These methods need the gradient of the function. They can compute it, but will perform better if you can pass them the gradient:

>>> deffprime(x):
... returnnp.array((-2*.5*(1-x[0])-4*x[0]*(x[1]-x[0]**2),2*(x[1]-x[0]**2)))
>>> optimize.fmin_cg(f,[2,2],fprime=fprime)
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 13
        Function evaluations: 30
        Gradient evaluations: 30
array([ 0.99999199,  0.99998336])

Note that the function has only been evaluated 30 times, compared to 120 without the gradient.

2.7.2.3. Newton and quasi-newton methods ¶

2.7.2.3.1. Newton methods: using the Hessian (2nd differential)¶

Newton methods use a local quadratic approximation to compute the jump direction. For this purpose, they rely on the 2 first derivative of the function: the gradient and the Hessian.

An ill-conditionned quadratic function:

Note that, as the quadratic approximation is exact, the Newton method is blazing fast

An ill-conditionned non-quadratic function:

Here we are optimizing a Gaussian, which is always below its quadratic approximation. As a result, the Newton method overshoots and leads to oscillations.

An ill-conditionned very non-quadratic function:

In scipy, the Newton method for optimization is implemented in scipy.optimize.fmin_ncg() (cg here refers to that fact that an inner operation, the inversion of the Hessian, is performed by conjugate gradient). scipy.optimize.fmin_tnc() can be use for constraint problems, although it is less versatile:

>>> deff(x):# The rosenbrock function
... return.5*(1-x[0])**2+(x[1]-x[0]**2)**2
>>> deffprime(x):
... returnnp.array((-2*.5*(1-x[0])-4*x[0]*(x[1]-x[0]**2),2*(x[1]-x[0]**2)))
>>> optimize.fmin_ncg(f,[2,2],fprime=fprime)
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 9
        Function evaluations: 11
        Gradient evaluations: 51
        Hessian evaluations: 0
array([ 1.,  1.])

Note that compared to a conjugate gradient (above), Newton’s method has required less function evaluations, but more gradient evaluations, as it uses it to approximate the Hessian. Let’s compute the Hessian and pass it to the algorithm:

>>> defhessian(x):# Computed with sympy
... returnnp.array(((1-4*x[1]+12*x[0]**2,-4*x[0]),(-4*x[0],2)))
>>> optimize.fmin_ncg(f,[2,2],fprime=fprime,fhess=hessian)
Optimization terminated successfully.
        Current function value: 0.000000
        Iterations: 9
        Function evaluations: 11
        Gradient evaluations: 19
        Hessian evaluations: 9
array([ 1.,  1.])

Note

At very high-dimension, the inversion of the Hessian can be costly and unstable (large scale > 250).

Note

Newton optimizers should not to be confused with Newton’s root finding method, based on the same principles, scipy.optimize.newton().

2.7.2.3.2. Quasi-Newton methods: approximating the Hessian on the fly¶

BFGS: BFGS (Broyden-Fletcher-Goldfarb-Shanno algorithm) refines at each step an approximation of the Hessian.

An ill-conditionned quadratic function:

On a exactly quadratic function, BFGS is not as fast as Newton’s method, but still very fast.

An ill-conditionned non-quadratic function:

Here BFGS does better than Newton, as its empirical estimate of the curvature is better than that given by the Hessian.

An ill-conditionned very non-quadratic function:

>>> deff(x):# The rosenbrock function
... return.5*(1-x[0])**2+(x[1]-x[0]**2)**2
>>> deffprime(x):
... returnnp.array((-2*.5*(1-x[0])-4*x[0]*(x[1]-x[0]**2),2*(x[1]-x[0]**2)))
>>> optimize.fmin_bfgs(f,[2,2],fprime=fprime)
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 16
         Function evaluations: 24
         Gradient evaluations: 24
array([ 1.00000017,  1.00000026])

L-BFGS: Limited-memory BFGS Sits between BFGS and conjugate gradient: in very high dimensions (> 250) the Hessian matrix is too costly to compute and invert. L-BFGS keeps a low-rank version. In addition, the scipy version, scipy.optimize.fmin_l_bfgs_b(), includes box bounds:

>>> deff(x):# The rosenbrock function
... return.5*(1-x[0])**2+(x[1]-x[0]**2)**2
>>> deffprime(x):
... returnnp.array((-2*.5*(1-x[0])-4*x[0]*(x[1]-x[0]**2),2*(x[1]-x[0]**2)))
>>> optimize.fmin_l_bfgs_b(f,[2,2],fprime=fprime)
(array([ 1.00000005,  1.00000009]), 1.4417677473011859e-15, {...})

Note

If you do not specify the gradient to the L-BFGS solver, you need to add approx_grad=1

2.7.2.4. Gradient-less methods ¶

2.7.2.4.1. A shooting method: the Powell algorithm¶

Almost a gradient approach

An ill-conditionned quadratic function:

Powell’s method isn’t too sensitive to local ill-conditionning in low dimensions

An ill-conditionned very non-quadratic function:

2.7.2.4.2. Simplex method: the Nelder-Mead¶

The Nelder-Mead algorithms is a generalization of dichotomy approaches to high-dimensional spaces. The algorithm works by refining a simplex, the generalization of intervals and triangles to high-dimensional spaces, to bracket the minimum.

Strong points: it is robust to noise, as it does not rely on computing gradients. Thus it can work on functions that are not locally smooth such as experimental data points, as long as they display a large-scale bell-shape behavior. However it is slower than gradient-based methods on smooth, non-noisy functions.

An ill-conditionned non-quadratic function:
An ill-conditionned very non-quadratic function:

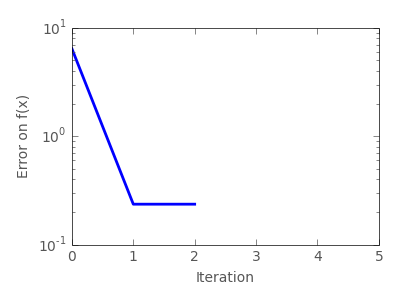
In scipy, scipy.optimize.fmin() implements the Nelder-Mead approach:

>>> deff(x):# The rosenbrock function
... return.5*(1-x[0])**2+(x[1]-x[0]**2)**2
>>> optimize.fmin(f,[2,2])
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 46
         Function evaluations: 91
array([ 0.99998568,  0.99996682])

2.7.2.5. Global optimizers ¶

If your problem does not admit a unique local minimum (which can be hard to test unless the function is convex), and you do not have prior information to initialize the optimization close to the solution, you may need a global optimizer.

2.7.2.5.1. Brute force: a grid search¶

scipy.optimize.brute() evaluates the function on a given grid of parameters and returns the parameters corresponding to the minimum value. The parameters are specified with ranges given to numpy.mgrid. By default, 20 steps are taken in each direction:

>>> deff(x):# The rosenbrock function
... return.5*(1-x[0])**2+(x[1]-x[0]**2)**2
>>> optimize.brute(f,((-1,2),(-1,2)))
array([ 1.00001462,  1.00001547])

2.7.3. Practical guide to optimization with scipy ¶

2.7.3.1. Choosing a method ¶

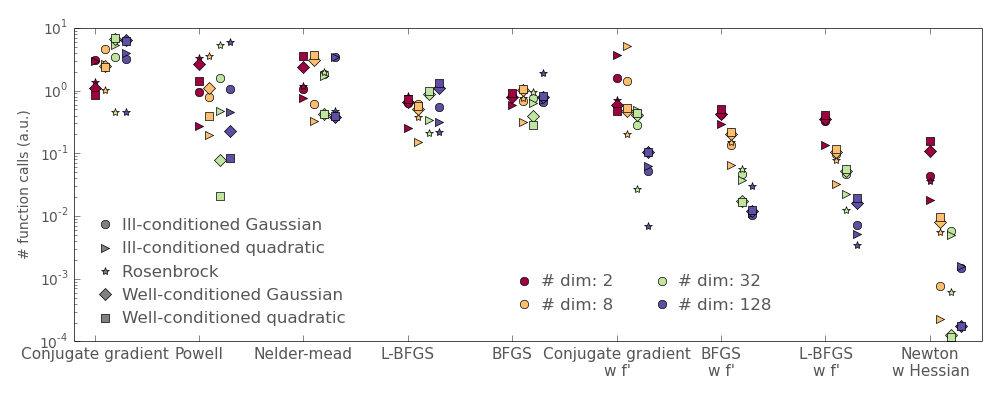
../../_images/plot_compare_optimizers_1.png

Without knowledge of the gradient:
	In general, prefer BFGS (`scipy.optimize.fmin_bfgs()`) or L-BFGS (`scipy.optimize.fmin_l_bfgs_b()`), even if you have to approximate numerically gradients On well-conditioned problems, Powell (`scipy.optimize.fmin_powell()`) and Nelder-Mead (`scipy.optimize.fmin()`), both gradient-free methods, work well in high dimension, but they collapse for ill-conditioned problems.
With knowledge of the gradient:
	BFGS (`scipy.optimize.fmin_bfgs()`) or L-BFGS (`scipy.optimize.fmin_l_bfgs_b()`). Computational overhead of BFGS is larger than that L-BFGS, itself larger than that of conjugate gradient. On the other side, BFGS usually needs less function evaluations than CG. Thus conjugate gradient method is better than BFGS at optimizing computationally cheap functions.
With the Hessian:
	If you can compute the Hessian, prefer the Newton method (`scipy.optimize.fmin_ncg()`).
If you have noisy measurements:
	Use Nelder-Mead (`scipy.optimize.fmin()`) or Powell (`scipy.optimize.fmin_powell()`).

2.7.3.2. Making your optimizer faster ¶

Choose the right method (see above), do compute analytically the gradient and Hessian, if you can.
Use preconditionning when possible.
Choose your initialization points wisely. For instance, if you are running many similar optimizations, warm-restart one with the results of another.
Relax the tolerance if you don’t need precision

2.7.3.3. Computing gradients ¶

Computing gradients, and even more Hessians, is very tedious but worth the effort. Symbolic computation with Sympy may come in handy.

Warning

A very common source of optimization not converging well is human error in the computation of the gradient. You can use scipy.optimize.check_grad() to check that your gradient is correct. It returns the norm of the different between the gradient given, and a gradient computed numerically:

>>> optimize.check_grad(f,fprime,[2,2])
2.384185791015625e-07

See also scipy.optimize.approx_fprime() to find your errors.

2.7.3.4. Synthetic exercices ¶

../../_images/plot_exercise_ill_conditioned_1.png

Exercice: A simple (?) quadratic function

Optimize the following function, using K[0] as a starting point:

np.random.seed(0)
K=np.random.normal(size=(100,100))
deff(x):
returnnp.sum((np.dot(K,x-1))**2)+np.sum(x**2)**2

Time your approach. Find the fastest approach. Why is BFGS not working well?

Exercice: A locally flat minimum

Consider the function exp(-1/(.1*x**2 + y**2). This function admits a minimum in (0, 0). Starting from an initialization at (1, 1), try to get within 1e-8 of this minimum point.

2.7.4. Special case: non-linear least-squares ¶

2.7.4.1. Minimizing the norm of a vector function ¶

Least square problems, minimizing the norm of a vector function, have a specific structure that can be used in the Levenberg–Marquardt algorithm implemented in scipy.optimize.leastsq().

Lets try to minimize the norm of the following vectorial function:

>>> deff(x):
... returnnp.arctan(x)-np.arctan(np.linspace(0,1,len(x)))
>>> x0=np.zeros(10)
>>> optimize.leastsq(f,x0)
(array([ 0.        ,  0.11111111,  0.22222222,  0.33333333,  0.44444444,
        0.55555556,  0.66666667,  0.77777778,  0.88888889,  1.        ]), 2)

This took 67 function evaluations (check it with ‘full_output=1’). What if we compute the norm ourselves and use a good generic optimizer (BFGS):

>>> defg(x):
... returnnp.sum(f(x)**2)
>>> optimize.fmin_bfgs(g,x0)
Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 11
         Function evaluations: 144
         Gradient evaluations: 12
array([ -7.4...-09,   1.1...e-01,   2.2...e-01,
         3.3...e-01,   4.4...e-01,   5.5...e-01,
         6.6...e-01,   7.7...e-01,   8.8...e-01,
         1.0...e+00])

BFGS needs more function calls, and gives a less precise result.

Note

leastsq is interesting compared to BFGS only if the dimensionality of the output vector is large, and larger than the number of parameters to optimize.

Warning

If the function is linear, this is a linear-algebra problem, and should be solved with scipy.linalg.lstsq().

2.7.4.2. Curve fitting ¶

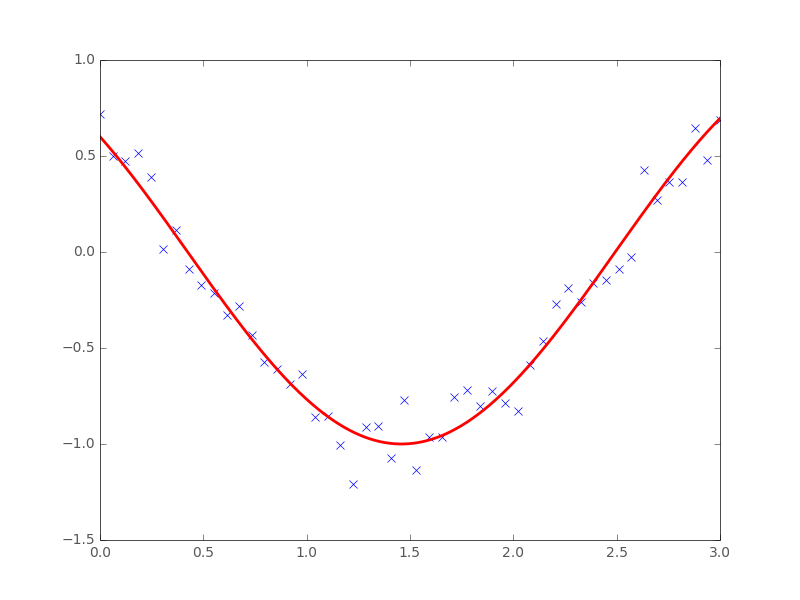
Least square problems occur often when fitting a non-linear to data. While it is possible to construct our optimization problem ourselves, scipy provides a helper function for this purpose: scipy.optimize.curve_fit():

>>> deff(t,omega,phi):
... returnnp.cos(omega*t+phi)
>>> x=np.linspace(0,3,50)
>>> y=f(x,1.5,1)+.1*np.random.normal(size=50)
>>> optimize.curve_fit(f,x,y)
(array([ 1.51854577,  0.92665541]), array([[ 0.00037994, -0.00056796],
       [-0.00056796,  0.00123978]]))

Exercise

Do the same with omega = 3. What is the difficulty?

2.7.5. Optimization with constraints ¶

2.7.5.1. Box bounds ¶

Box bounds correspond to limiting each of the individual parameters of the optimization. Note that some problems that are not originally written as box bounds can be rewritten as such via change of variables.

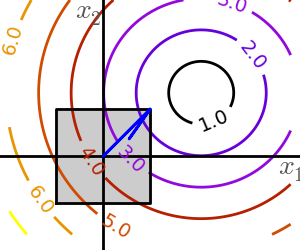
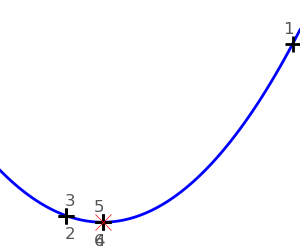
scipy.optimize.fminbound() for 1D-optimization

scipy.optimize.fmin_l_bfgs_b() a quasi-Newton method with bound constraints:

>>> deff(x):
... returnnp.sqrt((x[0]-3)**2+(x[1]-2)**2)
>>> optimize.fmin_l_bfgs_b(f,np.array([0,0]),approx_grad=1,bounds=((-1.5,1.5),(-1.5,1.5)))
(array([ 1.5,  1.5]), 1.5811388300841898, {...})

2.7.5.2. General constraints ¶

Equality and inequality constraints specified as functions: f(x) = 0 and g(x)< 0.

scipy.optimize.fmin_slsqp() Sequential least square programming: equality and inequality constraints: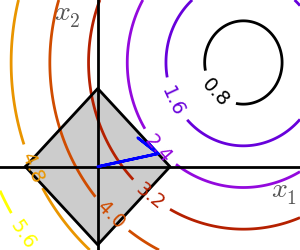

../../_images/plot_non_bounds_constraints_1.png

>>> deff(x):
... returnnp.sqrt((x[0]-3)**2+(x[1]-2)**2)
>>> defconstraint(x):
... returnnp.atleast_1d(1.5-np.sum(np.abs(x)))
>>> optimize.fmin_slsqp(f,np.array([0,0]),ieqcons=[constraint,])
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 2.47487373504
            Iterations: 5
            Function evaluations: 20
            Gradient evaluations: 5
array([ 1.25004696,  0.24995304])

scipy.optimize.fmin_cobyla() Constraints optimization by linear approximation: inequality constraints only:
```
>>> optimize.fmin_cobyla(f, np.array([0, 0]), cons=constraint)
array([ 1.25009622,  0.24990378])
```

Warning

The above problem is known as the Lasso problem in statistics, and there exists very efficient solvers for it (for instance in scikit-learn). In general do not use generic solvers when specific ones exist.

Lagrange multipliers

If you are ready to do a bit of math, many constrained optimization problems can be converted to non-constrained optimization problems using a mathematical trick known as Lagrange multipliers.